1980년에는 분명히 주기율표를 외우고 있었을 것이다. 무엇인지 모르고. 주기율표 the periodic table of elements에는 원소element가 나열되어 있고, 지금 다루는 것은 원자atom다. 원소는 뭐고, 원자는 무엇인가?
원소는 양성자수가 같은 원자들이다.
원자는 원자핵과 전자로 구성되어 있다.
원소로서의 수소는, 수소와 중수소라는 원자를 뜻한다. 또한, 수소와 중수소는 양성자수가 같은 동위원소로 각각 독립된 원자다. 즉, 수소라는 원자와 중수소라는 원자다. 물은 수소와 산소라는 원소로 구성되어 있고, 중수는 중수소(수소의 동위원소)와 산소라는 원자로 구성되어 있다.
아래 링크를 참조하여 원소와 원자를 구분해 본다.
https://chemielove.krict.re.kr/resources/images/book/book_atom_q13.pdf
물질의 구성요소에 대한 추정 : 헤라클레이토스(불), 탈레스(물), 데모크리토스(원자), 엠페도클레스(4원소설)
1803년 달톤의 원자론 : 질량 중심 정수비례의 법칙 - 산소 1개와 수소 2개가 모여 물을 만든다. 뉴턴 만유인력의 법칙의 응용.
멘델레에프 Менделеев의 원소 주기율표(질량 중심)에 대한 논문 발표(1869년, 러시아화학회) : 60개의 원소를 배열한다. 되베 라이너, 뉴랜즈 등 학자들의 연구업적을 종합하여 작업한 결과이다. 멘델레프는 주기율표를 만들고, 에카붕소(Sc), 에카 알루미늄(Ga), 에카실리콘(Ge)이 발견될 것이라는 예언을 했는데, 실제로 발견되었다. 1907년 노벨상 후보로 유력했으나, 사망하여 받지 못한다. eka는 산스크리트어로 1을 뜻한다.
요한 볼프강 되베 라이너 : 세쌍 원소설
: Li 7 - Na 23 - K 39의 원자량 비교. Li 와 K의 원자량 평균이 Na의 원자량이다.
: Ca 40 - Sr 88 - Ba 137의 원자량 비교
: Cl 35 - Br 80 - I 127의 원자량 비교
: 원자량으로 봤을때 주기 특성이 있다.
아래 동영상이 주기율표에 대한 고교 수준의 주기율표 설명인데, 엄청나게 많은 정보를 가지고 있다. 주기율표의 역사를 개관한 후에 기초를 다지는데 필요하다. 아, 고등학교 교과서다.
https://www.youtube.com/watch?v=s1-DTMNtst8
존 뉴랜즈의 옥타브 법칙 : 8개 마다 비슷한 속성을 가진 원소들이 나타난다는 주장. Li - Na - K이 비슷한 성질이라는 것을 밝혔다. 그가 작성한 주기율표가 불안하여 많은 학자들로부터 그의 논리가 배척을 받았으나, 멘델레예프의 주기율표가 왕립협회의 메달을 받게 되자, 이의 제기를 한 그에게도 왕립협회의 메달이 수여되었다고 한다.
7942 이사 가서 전화번호 57 - 567 - 3113 / 발헤 - XYZ - 리하슈불락 - 32 중성자 체드윅
1885 : 발머, 빛의 스펙트럼에 대한 공식
1887 : 헤르츠, 전자기파 발생 시험
1895 : 뢴트겐, X ray 발견
1896 : 베크렐, 우라늄 방사능 발견
1897 : J J 톰슨의 전자발견
1903 : 톰슨의 원자론 주장. 식빵 속의 건포도
1911 : 러더포드의 햇님계와 닮은 원자 생김새 주장 : 에너지를 잃으면 원자핵과 충돌하는 문제
1913 : 닐스 보어, 여러 에너지 궤도를 가진 원자 생김새 : 코펜하겐학파 - 하이젠베르크, 파울리
1924 : 파울리의 배타율 ; 드 브로이의 물질파
1925 : 하이젠베르크의 행렬-매트릭스 역학
1926 : 슈뢰딩거 방정식
1927 : 불확정설, 확률파 이론
1928 : 디락 방정식, 반물질 개념
1932 : 제임스 체드윅, 중성자 발견
1879 : 맥스웰이 죽고 아인슈타인이 태어난다
1642 : 갈릴레이가 죽고 뉴턴이 태어난다
1911년 뉴질랜드의 러더포드가 캠브리지 캐번디시연구소로 가서 알파입자를 쏘는 실험을 하여, 원자핵을 발견했다.
JJ 톰슨은 전자보다 천배 무거운 무엇이 있을 것이라고 추정했는데, 제자인 러더포드가 원자핵을 발견해 증명했다.
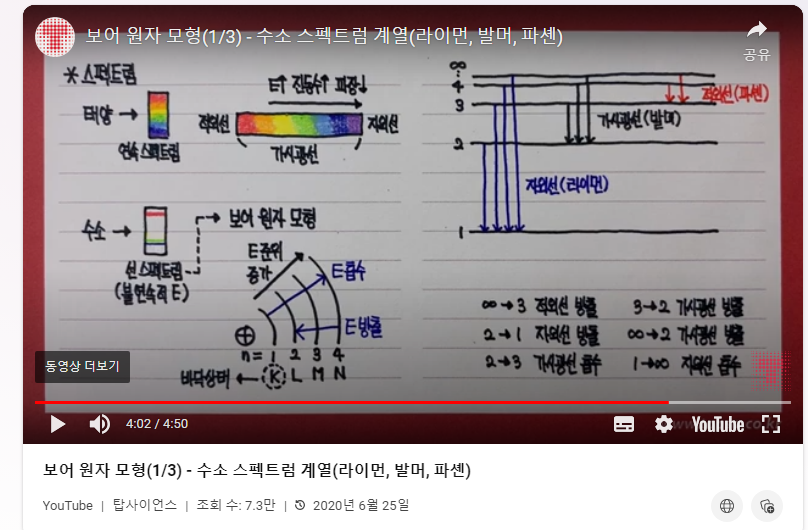
(1) 1885년 발머의 수소 원자의 스펙트럼 공식
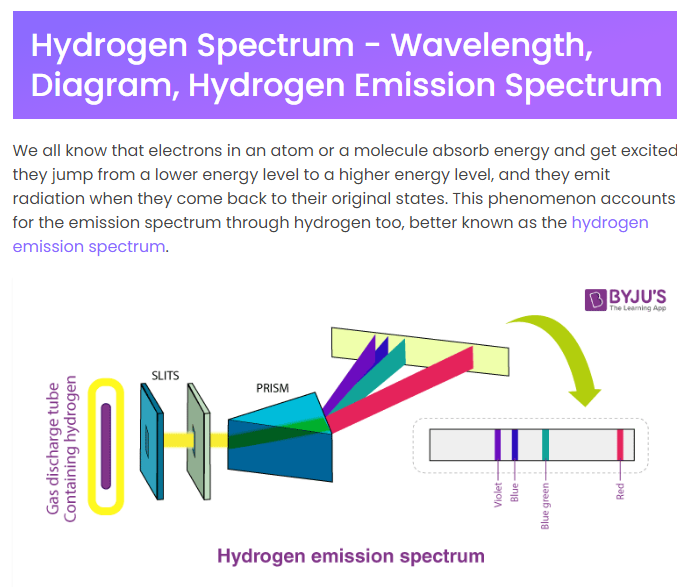
수소원자의 스펙트럼을 어떻게 관찰하는 것일까?
[화학1] 기체 방전관을 이용하여 선 스펙트럼 관찰하기(화학1 2단원. 원자의 세계, 스펙트럼 종류 알아보기, 선 스펙트럼과 연속 스펙트럼) (youtube.com)
수소기체에 에너지를 가하면 전자가 자신이 속해있던 껍질에서 다른 껍질로 이동을 했다가 원래 상태로 되돌아 가면서 빛을 방출한다. 이렇게 이해하자. 그런데, 흡수 스펙트럼이 있고 방출 스펙트럼이 있다고 한다. 위 영상의 스펙트럼은 방출 스펙트럼인가 흡수스펙트럼인가? 자료를 찾아보니 방출 스펙트럼이라고 한다.
"우리는 모두 원자나 분자의 전자가 에너지를 흡수하여, 낮은 에너지 껍질에서 높은 에너지 껍질로 뛰어오르고, 원래 상태로 돌아올 때 빛을 내보낸다는 것을 알고 있습니다. 이 현상은, 수소가 내보내는 스펙트럼, 즉 수소 방출 스펙트럼을 말한다."
뭘 알아보려고 찾을수록 의문이 쌓인다.
의문 1) Thomson의 음극선 실험은, 어떻게 식빵에 박힌 건포도 모양의 전자를 구상하게 했을까?
의문 2)
톰슨의 캐번디시랩의 제자인 러더포드는, 전자가 원자핵 주위를 도는 원자생김을 구상했다. 이 생김이 문제가 있다고 했는데, 왜 그랬을까? 아무 생각없이 그냥 지나쳤다.
오늘에야 그것이 중요한 문제인 것을 알겠다. 모든 운동하는 물질은 에너지가 계속 주어지거나 진공속이 아니라면 언젠가는 에너지를 잃게 된다. 즉, 원자핵 주위를 전자가 돈다고 생각하면, 원자는 존재할수가 없다. 원자에 어떻게 에너지를 주어서 전자를 계속해서 돌릴수 있다는 말인가? 힘을 잃은 전자는 원자핵에 끌려가서 꼼짝못하는 상태가 될수밖에 없다.
이중슬릿을 이용한 빛의 파장을 구하는 방법
https://www.youtube.com/watch?v=YgWQwFwu4KI
전제 1) B와 C의 두개 슬릿에서 동시에 떠나는 빛은 같은 파장을 가지고 있다. 출발점이 다른 똑같은 파장
전제 2) ∠CBG와 ∠POH는 같다. ∠POH가 더 크지만 d가 워낙 작은 값이라 거의 같다.
위 영상을 봤는데, 아직도 빈구석이 많다.
의문 1) 두개의 θ 값은 같지않다 : 위 전제2에 따라 두개의 θ 값은 같다.
의문 2) 이중슬릿을 통과한 빛이 만들어내는 보강과 소멸이 어떻게 식으로 표현되는지 알수 없다 : 파장이 맞으면 보강이 나타나고, 파장이 엇갈리면 소멸된다. 파장이 맞을때는 1파장 차이 - 2파장 차이 - 3파장 차이 - 4파장 - n파장 차이가 날때 보강간섭이 일어난다. 보강간섭이 일어나는 조건은, n λ = d sin θ
의문 3) 수소기체에 열을 가해서 이중슬릿을 통과시킨뒤 얻는 간섭무늬를 이용해 수소의 선스펙트럼의 파장을 구할수 있을까?
총 4개의 선이 나타나는데, 각각 n=1, 2, 3, 4일때 나타나는 선이다.
(2) 닐스 보어의 원자론
닐스보어는 러더포드의 실험을 옆에서 지켜보고 있다.
러더포드의 전자가 가진 문제를 해결하기 위해서는 껍질(궤도)를 만들면 된다.
각 궤도는 핵으로부터 n의 제곱만큼 떨어져 있다.
1, 4, 9, 16 ... 36, 49
전자의 에너지 껍질(n)은 총 7개가 있고,
7개 껍질을 벗어난 전자는 자유전자라 한다. 이 7개의 전자껍질이 주기율표의 주기다.
전자껍질은 외곽에 있을수록 에너지를 많이 가지고 있어서,
높은층에서 낮은층으로 내려올때 에너지를 빛으로 내보낸다. 주기율표가 빛이 되었다.
n=1 로 떨어지는 빛을 자외선
n=2 로 떨어지는 빛을 가시광선
n=3 로 떨어지는 빛을 적외선
놀라운 것은, 이것이 발머의 스펙트럼 공식과 맞아떨어진다.
(3) 슈뢰딩거 방정식
공간구조가 구조화되어 있다.
주기율표는 4개의 단지가 만들어져있다 => 슈뢰딩거 방정식 : 파동방정식 : 파동함수
확률로 존재한다. 하이젠베르크 불확정성의 원리.
각 운동량 angular moment
L0 (2칸) : I, II 족 (금속)
L1 (6칸) : III~VIII족
L2 (10칸) : 전이금속
L3 (14칸) : 희토류
L = n - 1 = 0, 1, 2, 3
nL : -1, 0, +1 : 왼쪽으로 회전, 무회전, 오른쪽으로 회전
±1
코펜하겐학파의 해석(막스 보른) : 파동을 확률로 보아야 한다. 전자가 존재할 확률로 봐야 한다.
(4) 디락 방정식 / 파울리 배타이론
spin up / spin dn : 배타이론에 따라 전자의 에너지 상태는 하나다.
상대성이론을 반영해야 한다.
입자가 존재하려면 공간이 필요하다. 불연속한 공간이 양자화 되어있다.
아날로그처럼 보이는 세상은, 해상도와 분해능이 떨어지기 때문에 연결된 것처럼 보인다.
세상은 디지털이다.
월말 김어준에서, 박문호는 멋있게 말하는 것은 해냈지만, 설명하는데 실패했다. 김어준이 너무 서둘렀다. 차분하게 더 따라갔으면, 정말로 멋지고 아름다운 것을 발견했을지도 모른다.
주기율표에 관한 박문호의 2019년 강의를 들었다. 1강 이곳에서 박문호가 파동함수를 설명하는 부분에서 서두르다보니 제대로 해내지 못했다. 2강에서는, 이 Cr과 Cu 부분을 설명하면서 제대로 해내지 못했다. 완벽하게 설명을 하려다가 무리한 건너뛰기를 하는 경우가 가끔 있으나, 박문호의 강의는 주의깊게 들어야 한다. 그것이 집중하는데, 오히려 도움이 된다. 언제쯤 무리하실까를 찾는 재미다.
Cr과 Cu는 에너지 높이를 가지고 설명하면 된다. 물론 나의 추정이다. 즉, 4s2보다 3d5나 3d10보다 에너지 높이가 낮기 때문에, 전자배열의 질서가 다른 것처럼 보이는 것이다. 3d1~4 보다 4s를 먼저 채우기 시작한 이유도 4s의 에너지 준위가 낮았기 때문이다.
https://youtu.be/tar2Eb2llrA?si=0zLfpNetHz1Zyqyn
원자번호 1번 수소에서 30번 Mn까지 전자껍질에 배치하는 방법대로 나타내면 아래 그림과 같다.
1s
2s 2p
3s 3p 3d
4s 4p 4d 4f
5s 5p 5d 5f 5g
6s 6p 6d 6f 6g 6h
7s 7p 7d 7f 7g 7h 7i
자

'호기심천국 > 영상과 함께 하는 호기심 천국' 카테고리의 다른 글
| 대기순환_250123 (0) | 2025.01.23 |
|---|---|
| [ 박문호 뇌과학 압축본 ] 뇌 그림을 모르고 어떻게 뇌를 이해하겠나_241201 el domingo, uno de diciembre_Воскресенье,один декабрь (0) | 2024.12.01 |
| [ 원자를 믿습니까 ] 볼츠만 이야기_원자의 존재를 이론물리학으로 증명하였다_241003 (0) | 2024.10.03 |
| [ 별의 거리를 측정하다 발견한 우주의 비밀_이강환_언더스탠딩 ] 연주시차와 레빗의 표준광원을 토대로 별의 거리를 측정하고, 커미의 가속팽창을 알아내다_240523 (0) | 2024.05.23 |
| 97년 위기 보다 더 큰 경제위기는 올 것인가_최배근 tv 159회_231112 (0) | 2023.11.12 |



