유튜브에 초등학교 경시대회에 나온 문제라며 올라와 있다.
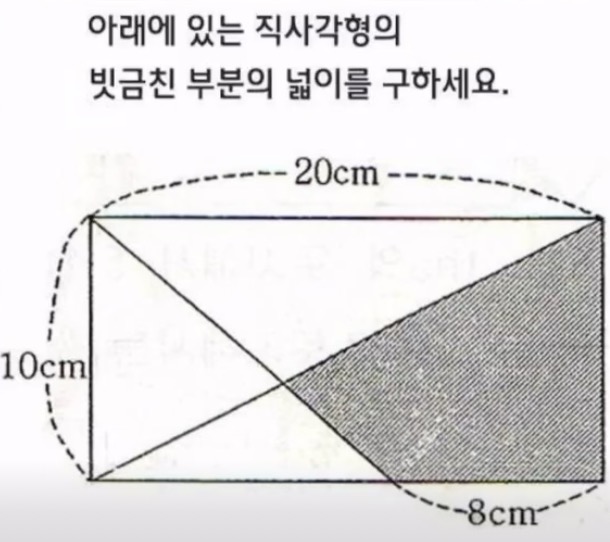
다사 대호는 다각형의 면적에 대한 비례법칙을 이용했고, 나는 보조선을 이용했다.
보조선을 이용하는 방법은 이해하기 쉽고 간단한 반면에 수식이 길다.

① 먼저 교차점 O를 지나는 수직선을 그어 높이를 h라고 한다.
② 면적 S = △BDE - △BCO = [ 1/2 x 20 x 10 ] - [ 1/2 x 12 x (10-h) ] = 100 - 6(10-h)
③ 면적 S = □ ACDE - △AEO = [ 1/2 x (8+20) x 10 ] - [ 1/2 x 20 x h ] = 140 - 10h
④ 100 - 6(10-h) = 140 - 10h
16h = 100
h = 25/4
⑤ h의 값을 ③에 대입하면,
S = 140 - 10 x 25/4
= 140 - 250/4 = 77.5㎠
다사 대호가 비례식을 이용해서 구하는 방법
① △CDE는 □ ABDE의 1/2 중 2/5 = 1/2 x 2/5 = 1/5 즉 □ ABDE의 1/5
② △AEO와 △CBO는 닮은꼴이므로 EO : BO = 20 : 12 = 5 : 3
③ △CEO는 [ □ ABDE의 1/2 중 3/5 ] 중 5/8 = 1/2 x 3/5 x 5/8 = 3/16 즉 □ ABDE의 3/16
④ 면적 S는 ① + ③이므로, □ ABDE의 면적 x (1/5 + 3/16) = 200 x 31/80 = 77.5㎠
재미있는 것은, 제미나이가 이것을 계산하지 못했다.

chat gpt는 문제를 풀었다. 방법은,
그림을 좌하단을 (0,0)으로 두고 직사각형을 (0,0),(20,0),(20,10),(0,10)이라 두자.
오른쪽 아래에서 8 cm 떨어진 점은 P(12,0).
두 선의 방정식
• BL\to TR:\ y=\frac12x
• TL\to P:\ y=10-\frac56x
교점 O는
\frac12x=10-\frac56x \Rightarrow x=7.5,\ y=3.75, 즉 O(7.5,3.75).
음영부는 사각형 TR(20,10)\to BR(20,0)\to P(12,0)\to O(7.5,3.75)의 넓이.
신발끈 공식으로
S=\tfrac12|20\cdot0+20\cdot0+12\cdot3.75+7.5\cdot10
-(10\cdot20+0\cdot12+0\cdot7.5+3.75\cdot20)|
=\tfrac12|120-275|=77.5
따라서 음영 부분의 넓이는 77.5\ \text{cm}^2.
chat gpt의 방법은 닮음비를 이용해 선분의 길이비를 구하고,
이것을 이용해 높이 10-h의 좌표를 구했다.
그 다음에는 삼각형의 면적을 구해서, 면적S를 구해야하는데,
신발끈의 공식이라는 알지못하는 부분으로 넘어간다.
뭘까? 정말로 구한것일까 아니면 거짓말을 하고 있는 것일까?
답을 어디서 구해온 다음에 과정을 멋대로 이어붙였다고 본다.
'호기심천국 > 영상과 함께 하는 호기심 천국' 카테고리의 다른 글
| [ 연대측정법 ] 기원은 커미의 방사선인 양성자다_260210 (0) | 2026.02.10 |
|---|---|
| [ 빅히스토리_산소없이 살아가는 사룸체가 있다_박문호 ] 지질을 하려다가 인지질로_250917 (0) | 2025.09.18 |
| [ 박문호_적혈구는 어디에서 만들어지는가_제3회 특별한 뇌과학_21년 ] 적혈구는 뼈에서 100%로 만들어진다_250616 (0) | 2025.06.17 |
| [ 월말 김어준 ] 지구의 역사는 포도당이다_24년 9월호_250312 (0) | 2025.03.12 |
| [ 대기순환 ] 햇빛이 적도지방을 달구면서 오름기류를 만든다_250123 (0) | 2025.01.23 |


